"Fibonacci Bivalve Equations"

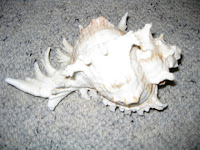
The Original Equation for crocheting or knitting a seashell was given in post:  21 June 2010 etc. 

F(n)  =  2 x F(n-2)  +  F(n-3)

F(n+1) = 2 x F(n-1) + F(n-2)  eg F9=34 = 2 x 13 + 8.........for knitting, work downwards, knit 2 together.
F(n) = 2 x F(n-2) + F(n-3)      eg F8=21= 2 x 8 + 5
F(n-1) = 2 x F(n-3) + F(n-4)   eg F7=13= 2 x 5 + 3...........for crocheting, work upwards, crochet twice in same loop.
Patterns are given for spiral seashells:-    23 June 2010, (here are the bivalves).
A green knitted bivalve and a red blue yellow crocheted bivalve were also configured from this Pattern.
***************************
The only bivalve made from the first Bivalve Pattern was a white crocheted  model.  23 June 2010.
At the time I guessed that one could knit  by working backwards;  later it was found to be not possible.
***************************
New Patterns are given recently:-      May 26 2011,  (the giant clam)
Diagrams and models  1 and 4 have a wavy lip like a clam.
Original working out is given in Fibonacci Fan shapes 1 to 610  and 233 to 6765.
Eventually a giant clam might be properly created- by someone- in fibre, iaw Fibonacci Series of numbers!
***************************

Here are the new Equations:-
From 1/2F(n) to knit next row 1/2F(n-1)
 = k2tog x 1/2 F(n-2) + k  1/2 F(n-3)
eg.  cast on 117.  k2tog x 45, k 27.  makes 72,  (nb. 0.5 is rounded off)
Fn=233,  F(n-2) is 89,  F(n-3) is 55, F(n-1) is 144.

From 1/2F(n-1) to crochet 1/2F(n)
= crochet 2x in loop x 1/2F(n-2) + crochet once in loops x 1/2F(n-3).
eg.  base 72 loops, crochet 2x  in next 45 loops, crochet once in 27 loops,  makes 117.
F(n-1)=144, F(n) is 233, F(n-2) is 89, F(n-3) is 55.

and so it goes, even if you were able to knit huge numbers:-
F59 is 956 722 026 041..........half is 478 361 013 020.5
F57 is 365 435 296 162..........half is 182 717 648 081
F56 is 225 851 433 717..........half is 112 925 716 858.5
..............................adding last two:-  295 643 364 939.5
.................which is half F58 ie half of 591 286 729 879
.......................................................................................
Equation was:-   from 1/2F59 make 1/2F58 by k2tog x 1/2F57 + k 1/2F56
......................................................................................
One can imagine a creature or single cell figuring out how to multiply its cells or molecules
or how to fuse or divide its cells or molecules to create a certain shape!
......................................................................................
i am in a bit of a hurry to publish my work in case i get sick.
28 lumps on my thyroid gland.
hands hurt so it is easier to type lower case.

I could type extensive Tables to prove my equations, as i did in posts dated 28 April 2011 etc.
but it could be that interested people might like to figure it out for themselves.
i have a big sheaf of handwritten numbers and the task has been to arrange them
 in reasonable presentation;  very easy to get muddled up....
This work was done in September 2010, so it has been a long time getting documented!
****************
A good friend taught me how to magnify a web page-  press ctl and +
To decrease size images,  press ctl and -
Thank you, Mark;  many of my Tables and diagrams are too small to see detail....

Real Seashells **

From glass cases in the Australian Museum, Sydney, and my friend's home,
 we have a collection of real seashells.

. 

More on the bivalves.**

Here are knitted models of the "bivalves" with various ways of configurating them.  Still the best way to make a giant clam is eluding me.  I might have to play around with it;  experiment.  Later.

The Giant Clam! **

Giant clam seen in scientists' room, upstairs at Australian Museum, Sydney.


Here begin efforts to create a mathematical hyperbolic model of a giant clam.
Jute twine was used, with  thick dowelling handmade knitting needles.
A new Pattern was used,  starring the number 9.
It was easy to crochet half of a bivalve, but not possible to knit it backwards,  thus a new Pattern was needed,  as described in the following images:-

You can click on these images to enlarge them, and to print them if need be.  Arrow back to return.

In fact, there are four different ways to organise the Pattern:-

You can see the wavy lip in bottom piece,  but it is still far from looking like the Real Thing.

This is Pattern for Crocheting Larger models of "Bivalve" = a great challenge for anyone to try.  My own work is not copyright, as far as I am concerned.  It belongs to Nature,  and we have the way to discover what we wish, according to our curiosity.  I do welcome the efforts of anyone who would like to try to elucidate secrets of our world.  Please share your results, especially students.  I hope these blog posts are of interest.  Thank you all.

------------------------Additional;  2/10/2015
To save a copy of any image, click on it to enlarge.
Then right click, and choose an option
eg save in downloads,
or copy then bring up a new Word page, click paste and save on computer.
or you can print.
_______________________________

New Models of Sea Snails, made last year, not shown until now. **

More Molluscs. **

It was in the section on Bivalves, 23/6/2010, that I wrote  "we have completed our work on molluscs".
There is actually much more!  Here again is the Pattern for crocheting  (and for knitting) a mollusc, even to an ambitious  degree of 4181.  If you click on the image it enlarges ok and you can print it or copy and save it to Word for your Reference as a Pattern that you can figure out for yourselves however you wish. 

If you increase crochet each row you get  a hyperbola starting from 1 and ending with an exceedingly frilly edge.  To make a cone, crochet one or more plain rows between each pattern row 

(or knit, working Pattern backwards, decreasing instead of increasing).
 
To make "ripples",  concentric circles with non frilly edge, you can go to the section with the maths on ripples etc,  (see Back Index at right,  April 17 2011 type 1),   to decide how wide to make the interval rows between pattern rows.  Circle circumference = 2 times Pi times radius.  Good luck.

Here below  is half section of a snailshell.  It was soaked in a thin aquadhere glue liquid and then dried before cutting in half with a sharp scalpel.  A real shell was halved with difficulty-  the shell is incredibly strong-  one has to bash it with a hammer.

The two sets of images following show the various configurations possible for a hyperbolic shape crocheted in yellow 8ply wool, I think it is, from memory,  using a number 10 crochet hook and treble stitch.

  (Usually I chose half treble.)  This time the looser stitch makes it more comfortable to adjust into different directions.           

The outside rows were of finer yarn-  987 row was in cream colour baby wool and the 1597 green row was crocheted in no. 8 crochet cotton.  I wanted to try to make the apex of the shell a finer, tighter coil.              

2,  7,  8,  Open hyperbolic fan shape

4,  "Stingray" shape,  made by folding in half and the again in half several times.

5,   "Chrysanthemun" shape, 

1,   Fold in half once, make clockwise spiral, just like a snail

9,  Fold in half once, make anticlockwise spiral;  this is not usually found in Nature.

3,  6,  16,  Top and bottom views of most easily arranged shapes made by continuing spirals from corners.

11,  14,  Two halves, front and back, one clockwise, one anticlockwise tight spirals.

10,  Outside of proper "Bivalve" configuration

14,  Inside of proper "Bivalve" configuration.

12,  15,  "Whelk" snail shape, configured and padded.

17,  :Snail" shape, padded.

18,  "Nautilus" shape, padded.

Photo is of Pelagic snail 

A cold and sunny winter's day, one year ago.

Camera had self timer and I had to run back quickly before the shutter went off!

I was working on this 1597 crochet model.

 

                                  

Of Mice ***nice video and music***

There is a bit of a mouse plague in our country region NSW Australia.
I caught 28 in traps before Easter.  I hate the killing and decided not to do so any more.
I clean up after the mice in my caravan.  One day I banged loud on a steel basin with a wooden spoon.
It was quiet for a few hours but that evening the mice went bananas!  Running everywhere!
I felt beaten, to say the least.  I racked my brains as to what I could do and I "asked" the mice something.
I "got" the answer when I made great effort to be CALM myself - and the mice calmed down too!
It was a nice quiet night.  Now I watch them,  and enjoy it, in my lovely life, to have some live company.

I am not a cat or dog person.  Indeed a one time male friend said to me "You are such a mouse!  Why don't you be an eagle?"  There is a story by Hyemenohost Storm about Hopping Mouse,  who became an eagle - by being EATEN.  My brother says he would rather I was able to befriend native mice, not the European ones.  My guess is that mice are mice - and are too similar -  just small diference in DNA maybe,  and in ancestry.....we are overrun with feral animals in Australia,  and native species from Australia have gone feral in other countries, with tragic results for original ecologies.

 Michael Roads can communicate with Nature and has written many books to inspire us.
He says that the forests that have been cut down-  they still exist in spiritual realm!

 If one human can do it, then it means that all of us are potentially able to do it also.  I feel that such ablity will help us with Plants also, and even with Fish and Molluscs and any Being alive.  Our true Nature is to be Custodians of this Beautiful Planet Earth.  I would like to do my utmost to try to find new ways to live this precious Life.
I may not succeed or survive,  but , then again,  I might well succeed,  and so may many of Us.
"Ganbatte, kudasai",  as the Japanese people so nobly say.
Please see http://www.ganbatte.org/  as a most appropriate link.

Surprise-

-the radio was playing just the right music while this scene was being recorded on my digital camera.  www.abc.net.au/classic  19/5/2011 I think.

Here is Shelly Mouse eating Cockle Creek Coal Cone-  Catamaran-  Recherche Bay  Tasmania.
(by courtesy of my brother Roger).   1/6/2011.

The Morning Stars Sing

Click once on image to enlarge, once again to enlarge more, then arrow back to return.
****sometimes it only works once....

The previous few mornings I have gone out at 5.15am and 6am to see the morning stars.

Jupiter and Venus are both glowing gold and I expect we shall see them for a number of months still until later they will be evening stars.

Mars was visible as red at 5am but was harder to see as the dawn crept on.

To Crochet a Cephalopod **

Nautilus belongs to the Phylum Mollusca -  it is a cephalopod,  a "head footed animal", related to squids and octopus.  A living fossil from 420 million years ago ( 265 million years before the dinosaurs), in the Lower Devonian  of the Paleozoic Era, it shared seas and oceans with ancient fishes, trilobites, brachiopods, crinoids, corals, gastropods, (the latter being "stomach footed animals").  It survived mass extinctions while the Ammonite species were all wiped out.  One book in the library had a picture of a Nautilus with a tall skinny spiral shape!

I drew this diagram, with info from net.

For a long time I presumed that the half section of seashell which adorns articles on the Fibonacci series to be that of a gastropod.  It was not until I saw a real Nautilus shell-  in a fabulous collection of huge seashells given to my friend Penny- that I realised it was not a spiral shell.  It is perfectly symmetrical both sides.
Back in this blog early on, I recounted how I thought how cool it would be to make a model of a Nautilus in accordance with the Fibonacci series.  One night I had an idea-  I leapt out of bed, switched on the torch and undid a crocheted snail model - and I managed to configure it into the yellow shape whose photo is under the black model! 

1597 stitches crocheted at outer  edge in the large model.
377 I think in the small model.
They are both made from the Hyperbolic shape Pattern
in accordance with the Fibonacci Series of numbers, described earlier.






My next drawing was made using the "pause" button on my portable DVD player:-

It is not possible to click to enlarge this image.  Maybe I have input too much data. The file size is presently 120KB after resizing as if  for email.  Before adding text it was 60.9KB.  Before resizing they were 3MB and 2.43MB.  I might have to redo the image with less text....  One needs a magnifying glass to read words!
It might be possible to select info, copy it and paste it into Word document, then edit it to be more readable.

It was quite wonderful to see film of Nautilus swimming in the Coral Reef DVD, purchased from the shop in the Australian Museum in Sydney. It is "Coral Sea Dreaming.  Awaken." 
See http://www.protectourcoralsea.org.au/
The makers of the film warn us that if oceans become acidic, then not only will calcareous shells of animals dissolve, also the eardrums of fishes such as whales and dolphins, made of calcium, will dissolve.

My feeling is that the best way we can save our world is to become peaceful ourselves, to be happy,  and that means all of us need to practise NO MATTER WHAT HAPPENS,  and to help each other. Any negativity only feeds the negative.
I know it is hard not to worry when the situation feels impossible.
 His Holiness The Dalai Lama says we need to Transform Ourselves, with Compassion.
We ARE so powerful -  the Siberian Wisewoman Anastasia declares so to us.
 Her supraparaphraseing of the Lord's Prayer begins
 "Our Father who is Everywhere,  I am Your Daughter;  Your Joy I Declare."
Them is beautiful words.

Fossil Ammonite from Australian Museum's display; my photo.

Below is photo of Australian Museum, Sydney facade, near Hyde Park.





The word "Nautilus" has for a long time captured the imagination of the world at large.
First there was "Twenty Thousand Leagues Under the Sea", by Jules Verne (1828 - 1905).
The "Nautilus" is the fictional submarine of Captain Nemo.
The film of the same name as the book starred James Mason, Kirk Douglas, Peter Lorre and .....
The battle with the giant squid was truly gripping!.
 A 3D version is being made.
Not only that, but astronomer David Reneke has a website and I subscribe to his newsletter. 
There is a multi mission space exploration vehicle, for the Moon and Mars,
 and its name is Nautilus - X 
 ie Non Atmospheric Universal Transport Intended for Lengthy United States Xploration. 
 See Wikipedia.

One last comment:-
I was lucky to find an article in the Sydney Morning Herald, regarding "Thinking Hyperbolically".
Feb 19, 2011.   Felix R  a student at Sydney's International Grammar School in Ultimo said how cool it is to see the maths underlying the world around us. ( I wish I had written down his exact words.)  Melissa Silk is the School's Head of Design and Jane Martin is Head of Maths.  Their students made nomographs from their names- fine art prints- exhibited at The Powerhouse Museum.

********************
21 July 2011
Making a model of Nautilus by rolling hyperbola shape up like a pancake is only half the story.
A more correct model would include the Septa which form up to 34 chambers.....
********************

Tribute to Helle **

Allow me to introduce one of my very favourite websites:-

http://www.hellejorgensen.typepad.com/

Helle has crocheted a Vortex out of yarn made from recycled plastic shopping bags. Full size is 3 metres length and 1.5 metres diameter at the top. See November 2007. Check out more by searching keyword "rubbish vortex".

I was delighted to see that Helle has discovered how to crochet a spiral galaxy- I do not know if iaw fib series or not! It was to do with beginning the crochet on her vortex.

March 2008 there is a photo of 5 black spiral eggs from the Port Jackson shark, Heterodontus portus jacksoni, found on the beach. I tried to crochet the same, see my blog here in June 2010.

Her crocheted coral reef hat is lovely, 9/5/2007, modelled by a beautiful young Russian lady who just happened to visit. There is also a pink flower hat.

Another creation of Helle's is a Crocheted Cephalopod! June 2010.

Bravo Helle! Thank you.

Equations for a Frilly Edge **

These will be added asap

Horns, tusks, fangs and thorns, spines and prickles **

All these structures are close to cone shapes, and can be pointy to the extreme. What is the point, literally, to having horns etc?

In the biodynamic agriculture of Rudolph Steiner the cow horn is used to make 500, the manure preparation in a cow's horn which is buried for months in the ground, and cosmic energies are collected. Later the horn is dug up, and the 500 is used in tiny amount in clean water and stirred making a vortex, then reversing the vortex, making chaos turbulence, then making vortex again, for one hour, then a fine spray is delivered unto the farm or garden.

Partly it is fine microbial inoculum which is delivered, but also cosmic energy.

In Australia, Alex Podolinsky has mentored many farmers.

Here we have cow horn and vortex, both subjects of this blog.

Many reference online to horns, tusks, fibonacci extol the connection; one by Donald E. Smamek calls it Fibonacci Flim Flam.

Here I would like to demonstrate a model which supports the mathematics.

I began with the huge project of making a snail, I thought , with many chambers, so I might need to go to F21 which is 10946. I used mercerised crochet cotton, size 40 and a No. 2 crochet hook and half treble stitch. At one point in the making I suspected it would not make a snail shape, but more likely a horn shape, and so it was to be.

The results are posted here but I have trouble organising the images on blog. They seem to go to top of page so I have to enter them in reverse order. Plus the spacing goes haywire and one has to scroll a long way down to get to some text. Sorry about that.

Also I have maths tables giving Equations! but the blog seems to be having a nervous breakdown downloading these, as you can see in the section on vortexes, so I will have to omit them and only briefly sketch them. With luck, a book might come out of all this!

The model before spiralling. looks like the brain and falls naturally into 2 hemispheres. It makes me wonder if the brain is actually made of a flat hyperbolic fan shape, all connected together.

Weird how brain and horn are intrinsically the same fibonacci model shape! Wonderful to wonder why animals need horns, apart from fighting etc.

We know that horns are hollow inside. Maybe the animal dissolves the inside as it grows, or maybe there is another process altogether!

I nearly broke both thumbs and blistered fingertips trying to make it all spiral. If I had used a treble or double treble stitch it might have been more easily flexible. As it is the 4 balls of cotton cost $30.

One image shows the model stretched out before spiralling. The frilly edge measures 21 metres and the equation which matches this is x= F(n-13) x 100000 / Fn where 1000 stitches measure 191.92 cm. The outer edge is F(n-13) metres, an exact fibonacci number if this thickness of yarn is used. My cotton made 208 cm for 1000 stitches, and this is close to 191.92.

There is another equation having F(n-10) if the yarn is thicker like wool! Next time.

There are many books out on fibonacci series, eg "Wild Fibonacci" a childrens book by Joy N. Hulme and illustrated in acrylic paintings by Carol Schwartz.